6.1.1 特異点解析

まずはじめに行うのが特異点解析です。 \eqref{asc Leg eq}の2回微分の係数を \(1\) にすると \[ \tag{6.2} \label{asc Leg eq monic} D^2y -\dfrac{2x}{(1-x)(1+x)}Dy + \left( \dfrac{\lambda}{(1-x)(1+x)} - \dfrac{m^2}{(1-x)^2(1+x)^2} \right) y =0 \] となります。 以降の議論の簡単のために、1回微分と0回微分の係数を \begin{array}{rcl} p(x) &=& -\dfrac{2x}{(1-x)(1+x)} \\ q(x) &=& \dfrac{\lambda}{(1-x)(1+x)} - \dfrac{m^2}{(1-x)^2(1+x)^2} \end{array} としておきましょう。 「\(p, q\) が共に正則」とならないのは、\(x=\pm1, \infty\) なのは一目瞭然ですね。

\(x=\pm1\) では \begin{array}{l} \lim_{x\to\pm1}|(x\pm1)p(x)|\lt\infty \\ \lim_{x\to\pm1}|(x\pm1)^2q(x)|\lt\infty \end{array} より、\(x=\pm1\) が確定特異点であることがわかります。

無限遠点の特異点解析は \(\xi=1/x\to0\) とするのが常套手段です。 \eqref{asc Leg eq}に \(\xi\) を代入して\eqref{asc Leg eq monic}同様に2階微分の係数を \(1\) とすれば、 \[ \dfrac{d^2y}{d\xi^2} + \dfrac{2\xi}{(\xi^2-1)} \dfrac{dy}{d\xi} + \left( \dfrac{\lambda}{\xi^2(\xi^2-1)} - \dfrac{m^2}{(\xi^2-1)^2} \right) y =0 \] が得られます。 従って \begin{array}{rl} \lim_{\xi\to0} & \xi \left| \dfrac{2\xi}{(\xi^2-1)} \right| \lt\infty \\ \lim_{\xi\to0} & \xi^2 \left| \dfrac{2\lambda}{\xi^2(\xi^2-1)} - \dfrac{m^2}{(\xi^2-1)^2} \right| \lt\infty \end{array} より、無限遠点も確定特異点であることがわかります。

6.1.2 原点周りの級数展開

§6.1.1 で見たように、ルジャンドル陪微分方程式の特異点は \(\pm1, \infty\) の3点に限られます。 特に原点は正則点ですから、原点周りでは解 \(P_\lambda^m\) をテイラー展開できます。

微分方程式の解は \[ y(x)=\sum_{k=0}^\infty a_kx^k \] の形で書けます。 ここで、原点から最も近い特異点 \(\pm1\) までの距離が \(1\) ですから、級数の収束半径は \(1\) ですね。

従ってはじめから \(x\lt1\) を仮定してもよく、\eqref{asc Leg eq}の0階微分の項が \[ \left( \lambda - \dfrac{m^2}{1-x^2} \right) y = \left( \lambda - m^2\sum_{n=0}^\infty x^2n \right) y \] となることに注意して、\eqref{asc Leg eq}に級数を代入すると、 \begin{array}{cl} & \displaystyle \sum_{k=2}^\infty k(k-1)a_kx^{k-2} + \sum_{k=0}^\infty [-k(k-1)-2k+\lambda]a_kx^k - \sum_{k,n=0}^\infty m^2a_kx^{k+2n} \\ =& \displaystyle y \left( (k+2)(k+1)a_{k+2} + [\lambda-k(k+1)]a_k - \sum_{n=0}^{[k/2]}m^2a_{k-2n} \right) x^k \end{array} です。

微分方程式\eqref{asc Leg eq}が常に満たされるには、\(x^k\) の係数がそれぞれ \(0\) すなわち \[ \tag{6.3} \label{recurrence} a_{k+2} = -\dfrac{\lambda-k(k+1)}{(k+2)(k+1)}a_k + \dfrac{m^2}{(k+2)(k+1)} \sum_{n=0}^{[k/2]}a_{k-2n} \] が必要です。 これがルジャンドルの陪微分方程式の級数の係数の関する漸化式になります。

\(a_k\) が \(k\) の偶奇で完全に独立であることに注意しましょう。 実際、はじめのいくつかを挙げると以下のようになります。 \begin{array}{rcl} a_2&=&\dfrac{-\lambda+m^2}{2}a_0 \\ a_3&=&\dfrac{-\lambda+2+m^2}{6}a_1 \\ a_4&=&\dfrac{-\lambda+6}{12}a_2+\dfrac{m^2}{12}(a_2+a_0) \\ a_5&=&\dfrac{-\lambda+30}{42}a_3+\dfrac{m^2}{42}(a_3+a_1) \end{array} ここからわかる通り、\(k\) が偶数なら \(a_k\) は \(a_0\) に、奇数なら \(a_1\) に比例しますね。

\eqreg{asc Leg eq}の解の級数展開は、漸化式\eqref{recurrence}によって得られる \(a_k\) を用いて \(\displaystyle\sum_{k=0}^\infty a_kx^k\) で与えられます。 \begin{cases} y_0&=&\displaystyle\sum_{k=0}^\infty a_{2k}x^{2k} &(a_0\neq0, a_1=0) \\ y_1&=&\displaystyle\sum_{k=0}^\infty a_{2k+1}x^{2k+1} &(a_0=0, a_1\neq0) \end{cases} \(y_0, y_1\) は共に\eqreg{asc Leg eq}の独立な2解になっていますから、ルジャンドルの陪微分方程式の一般解は \(y_0, y_1\) の線型結合で表されます。

より深く解析するために \(m=0\) すなわちルジャンドルの微分方程式の級数展開を考えてみましょう。 \eqref{recurrence}にて \(m=0\) を考えれば、 \[ \tag{6.4} \label{recurrence of Leg eq} a_{k+2} = -\dfrac{\lambda-k(k+1)}{(k+2)(k+1)}a_k \] です。 複素数 \(l\) を用いて \(\lambda=l(l+1)\) と表せば、 \[ \tag{6.5} \label{recurrence of Leg eq with l} a_{k+2} = -\dfrac{(l-k)(l+k+1)}{(k+2)(k+1)}a_k \] よって、 \begin{array}{rcl} a_{2k} &=& -\dfrac{(l-2k+2)(l+2k-1)}{2k(2k-1)}a_{2k-2} \\ &=& \cdots \\ &=& \dfrac{(-1)^;(l-2k+2)(l-2k+4)\cdots l\cdot(l+2k-1)(l+2k-3)\cdots(l+1)}{(2k)!}a_0 \\ a_{2k+1} &=& -\dfrac{(l-2k+3)(l+2k)}{2k(2k+1)}a_{2k-1} \\ &=& \cdots \\ &=& \dfrac{(-1)^;(l-2k+3)(l-2k+5)\cdots(l+1)\cdot(l+2k)(l+2k-2)\cdots(l+2)}{(2k+1)!}a_1 \end{array} が得られます。

特に \(l\in\mathbb{Z}\) のとき、\eqref{recurrence of Leg eq with l}の \((l-k)(l+k+1)\) の効果によって \(a_{k_0}=0\) なる \(k_0\in\mathbb{Z}_{\geq0}\) が存在します。 かくなる \(k_0\) に対し、\(a_{k_0+2}=a_{k_0+4}=\cdots=0\) ですから、係数は偶奇いずれかが途中で断絶しますね。 つまりルジャンドルの微分方程式の特解が多項式で与えられます。

この係数が途中で断絶した多項式は一般に「第1種ルジャンドル関数」「ルジャンドル多項式」などと呼ばれます。 その具体形に関しては、より簡潔な形で表すことができますから、追々みていくことにしましょう。 多項式の解と独立な解、すなわち第1種ルジャンドル関数と偶奇が異なる解は、係数が打ち止めされず無限級数になりますね。 この無限級数は一般に「第2種ルジャンドル関数」などと呼ばれます。

6.2.1 関数の直交性

関数が直交するということについて考える前に、まずはベクトルの直行性を思い出しておきましょう。 ベクトル \(\boldsymbol{u}=(u_1, u_2, \cdots), \boldsymbol{v}=(v_1, v_2, \cdots)\) があったとき、これらが直交するとは \[ (\boldsymbol{u},\boldsymbol{v}) := \sum_i u_iv_i =0 \] で定義されるのでした。 すなわちベクトルが \(i=1,2,\cdots\) によってラベリングされており、各ラベルについて積を取って足し上げるというものだったわけです。

これを関数の直交性に援用します。 区間 \(I\) 上の関数 \(f(x), g(x)\) は \(x\) によってラベリングされていると考えると、 \[ (f,g) := \int_I f(x)g(x)dx =0 \] とすればよさそうです。

しかし、内積の定義には双線型性 \((f,\lambda g)=(\lambda f, g)=\lambda(f,g)\) と正値性 \((f,f)\geq0\) が必要であり、上記の定義では \(f(x), g(x)\) が複素数値を取ったとき (例えば \(f(x)=g(x)=i\) のとき) に正値性を満たしません。 そこで左側の関数について複素共役をとり、 \[ (f,g) := \int_I f^\ast(x)g(x)dx =0 \] と定義してあげます。 電磁気など実数値関数しか使わない場面において複素共役は不要ですが、量子力学を含め一般の議論では必要不可欠であることに注意しましょう。

6.2.2 ルジャンドルの陪微分方程式の解における直交性の証明

それではルジャンドル陪微分方程式の解に直交性があることを示していきます。

線形微分方程式の解が直交であることの証明では、\(L_{\lambda'}^m[y_{\lambda'}^m]=0\) を使って \[ \int(y_\lambda^m)^\ast L_{\lambda'}^m[y_{\lambda'}^m]dx=0 \] とするのが常套手段です。 部分積分を用いて計算すると、 \begin{array}{rcl} 0 &=& \displaystyle \int_{-1}^1 (y_\lambda^m)^\ast \left[ D \left( (1-x^2)Dy_{\lambda'}^m \right) + \lambda'y_{\lambda'}^m - \dfrac{m^2}{1-x^2}y_{\lambda'}^m \right] dx \\ &=& \displaystyle \left[ (y_\lambda^m)^\ast (1-x^2) Dy_{\lambda'}^m \right]_{x=-1}^{x=1} + \int_{-1}^1 \left[ (x^2-1) (Dy_\lambda^m)^\ast Dy_{\lambda'}^m + \left( \lambda' - \dfrac{m^2}{1-x^2} \right) (y_\lambda^m)^\ast y_{\lambda'}^m \right] dx \\ &=& \displaystyle \left[ (x^2-1) (Dy_\lambda^m)^\ast y_{\lambda'}^m \right]_{x=-1}^{x=1} + \int_{-1}^1 \left[ -D [(x^2-1)(Dy_\lambda^m)^\ast] y_{\lambda'}^m + \left( \lambda' - \dfrac{m^2}{1-x^2} \right) (y_\lambda^m)^\ast y_{\lambda'}^m \right] dx \\ &=& \displaystyle (\lambda'-\lambda) \int_{-1}^1 (y_\lambda^m)^\ast y_{\lambda'}^m dx \qquad\because(5.13) \end{array} となります。 \(\lambda\neq\lambda'\) のときは積分が \(0\) となるので、直交性が示されました。

6.3.1 \(\phi\) に関する一般的な境界条件と \(m\) の制限

はじめに、解が求まっている \(\Phi(\varphi)\) について一般に要求される境界 条件を与えることで、\(m\) の値を絞っていきます。

§4で挙げたような状況では基本的に \(\varphi\to\varphi+2\pi\) としても不変であることが要求されます。 これは(5.15)が \(\varphi\to\varphi+2\pi\) の変換で不変、すなわち \(\phi\) の値がただ一つに定まる (1価関数になる) というものです。

従って複号同順で \[ \Phi(\varphi)=\Phi(\varphi+2\pi) \qquad i.e.\qquad e^{\pm im\varphi} = e^{\pm im\varphi} e^{\pm 2\pi mi} \] となるので、 \[ \tag{6.7} \label{m in Z} m\in\mathbb{Z} \] に限られます。

6.3.2 \(\theta\) に関するルジャンドルの微分方程式の一般的な境界条件と \(\lambda\) の制限

一般に与えられるもう一つの条件として、\(0\leq\theta\leq\pi\) にて \(\phi\) が正則 (値が発散しない) というものがあります。

この条件を求めるために、\(\theta\approx0,\pi\) での挙動を調べましょう。 いきなり一般の \(m\in\mathbb{Z}\) について調べるのは難しいので、はじめは \(m=0\) のルジャンドルの微分方程式における条件を見ていきます。

\eqref{recurrence of Leg eq}において \(k\to\infty\) を考えると \(a_{k+2}\approx a_k\) ですね。 \(x\to\pm1\) を考えると、\(a_l=0\) となる \(l\in\mathbb{Z}_{\geq0}\) がなければ、 \begin{array}{rcl} y_\lambda(x\to\pm1) &=& \lim_{n\to\infty} \sum_{k=0}^n (a_{2k}\pm a_{2k+1}) \\ &\approx& \lim_{n\to\infty} (2ka_{2k}\pm(2k+1)a_{2k+1}) \end{array} となってしまいます。 (5.9)の \(x=\cos\theta\) は \(1\) にも \(-1\) にもなることを考えれば、係数 \(a_0\) はどこかしらで打ち止めされていなければなりません。 従ってルジャンドルの微分方程式の解が正則であるためには、級数展開の係数\eqref{recurrence of Leg eq}が \[ \exists l\in\mathbb{Z}_{\geq0} \quad s.t.\quad a_{l+2} = -\dfrac{\lambda-l(l+1)}{(l+2)(l+1)} =0 \] を満たすことが要求されます。 ゆえに \[ \lambda=l(l+1)\qquad(l\in\mathbb{Z}_{\geq0}) \] が必要となりますね。

6.3.3 \(\theta\) に関するルジャンドルの陪微分方程式の一般的な境界条件と \(\lambda\) の制限

一般の \(m\) については、実際に解を構成してからでないと条件を示すのが困難です。 ここでは天下りになりますが、後に§7.3で与えるルジャンドル陪多項式を特解として認め、議論を進めていきます。

出発点は(5.10)を移項した固有方程式 \[ \tag{6.9} \label{asc Leg eq for lambda constraint} \left( D((1-x^2)D) - \dfrac{m^2}{(x+1)(x-1)} \right) y\lambda^m = -\lambda y_\lambda^m \] です。

与えられた \(m\) に対して異なる固有値 \(\lambda\lt\lambda'\) を与える固有関数 \(y_\lambda^m, y_{\lambda'}^m\) を用いて、

1. \(y_{\lambda'}^m\) の零点の数は \(y_\lambda^m\) より多いことを示す
2. \(\lambda-l(l+1)\) のときに、特解であるルジャンドル陪多項式の零点が高々 \(l-m\) 個しかないことを示す

の手順で条件を導きます。

手順1

\(x=\pm1\) で正則な解が \[ y_\lambda^m(x) = (x\mp1)^\mu \sum_{k\in\mathbb{Z}_{\geq0}} a_k(x\mp1)^k \qquad (\mu\in\mathbb{Z}_{\geq0}) \] と展開されるとして代入すると、\(x\approx\pm1\) で最低次の項は \[ \mu(\mu-1)(x\mp1)^{\mu-2} + \dfrac{2\cdot(\pm1)}{\pm2(x\mp1)} \mu(x\mp1)^{\mu-1} - \dfrac{m^2}{4} (x\mp1)^{\mu-2} + O((x\mp1)^{\mu+1}) \approx \dfrac{\lambda}{\pm2} (x\mp1)^{\mu-1} \] である。 微分方程式が成り立つには左辺の係数が \(0\) すなわち \[ \mu(\mu-1) + \mu - \dfrac{m^2}{4} = 0 \quad i.e.\quad \mu=\pm\dfrac{m}{2} \] が得られます。

ここでは \(\mu\) の具体形を求めるよりも、\(\mu\geq0\) となる解が存在することを使う。 以下度々 \((x+1)^{|m|/2}\) という形式が現れるが、どれも「負冪でない関数」と捉えておけば十分でsる。

\(\lambda\lt\lambda'\) のもとで異なる固有方程式の解 \(y_\lambda^m, y_{\lambda'}^m\) が \(x=-1\) で正則としましょう。 すなわち \(y_\lambda^m, y_{\lambda'}^m\) はそれぞれ \begin{cases} \left( D((1-x^2)D)-\dfrac{m^2}{(x-1)(x+1)} \right) y_\lambda^m = -\lambda y_\lambda^m \\ \left( D((1-x^2)D)-\dfrac{m^2}{(x-1)(x+1)} \right) y_{\lambda'}^m = -\lambda y_{\lambda'}^m \end{cases} を満たし、またテイラー展開できて \begin{array}{} \displaystyle y_\lambda^m(x=-1) = \left[ (x+1)^{|m|/2} \sum_{k=0}^\infty a_k(x+1)^k \right]_{x=-1} = 0 \\ \displaystyle y_{\lambda'}^m(x=-1) = \left[ (x+1)^{|m|/2} \sum_{k=0}^\infty a_k'(x+1)^k \right]_{x=-1} = 0 \end{array} です。 固有方程式の両辺にスカラーをかければわかる通り、固有関数のスカラー倍も固有関数ですから、先頭の係数を \(a_0=a_0'=1\) とすることができます。 このとき \(y_\lambda^m, y_{\lambda'}^m\approx(x+1)^{|m|/2}\) なので、\(Dy_\lambda^m(x=-1), Dy_{\lambda'}^m(x=-1)>0\) となります。

この条件下で \(y_\lambda^m\) の零点 \(-1\) とその次の零点 \(x_0\) との間に、\(y_{\lambda'}^m\) は零点を持つことを背理法で証明します。 ロンスキアンを \[ \tag{6.10} \label{Wronskian} W := (1-x^2) \left( y_{\lambda'}^m Dy_\lambda^m - y_\lambda^m Dy_{\lambda'}^m \right) \] で定めます。

関数列 \(\{f_i(x)\}_{i=1,2,\cdots}\) のロンスキアンは一般には \[ \left| \begin{matrix} f_1 & f_2 & \cdots \\ f_1'(x) & f_2'(x) & \cdots \\ f_1''(x) & f_2''(x) & \cdots \\ \vdots & \vdots & \ddots \end{matrix} \right| \] で定義されるが、今回は固有方程式による変形を見込んで係数に \(1-x^2\) を付している。

これで \(x\) を微分すると \begin{array}{rcl} DW &=& D[ y_{\lambda'}^m\cdot(1-x^2)Dy_\lambda^m - y_\lambda\cdot(1-x^2)Dy_{\lambda'}^m ] \\ &=& Dy_{\lambda'}^m\cdot(1-x^2)Dy_\lambda^m + y_{\lambda'}^mD[(1-x^2)Dy_\lambda^m] - Dy_{\lambda'}^m - y_\lambda^mD[(1-x^2)Dy_{\lambda'}^m] \\ &=& -y_{\lambda'}^m\lambda y_\lambda^m + y_{\lambda'}^m\dfrac{m^2}{x^2-1}y_\lambda^m + y_\lambda^m\lambda'y_{\lambda'}^m - y_\lambda^m\dfrac{m^2}{x^2-1}y_{\lambda'}^m \quad\because\eqref{asc Leg eq for lambda constraint} \\ &=& (\lambda'-\lambda)y_\lambda^my_{\lambda'}^m \end{array} となります。

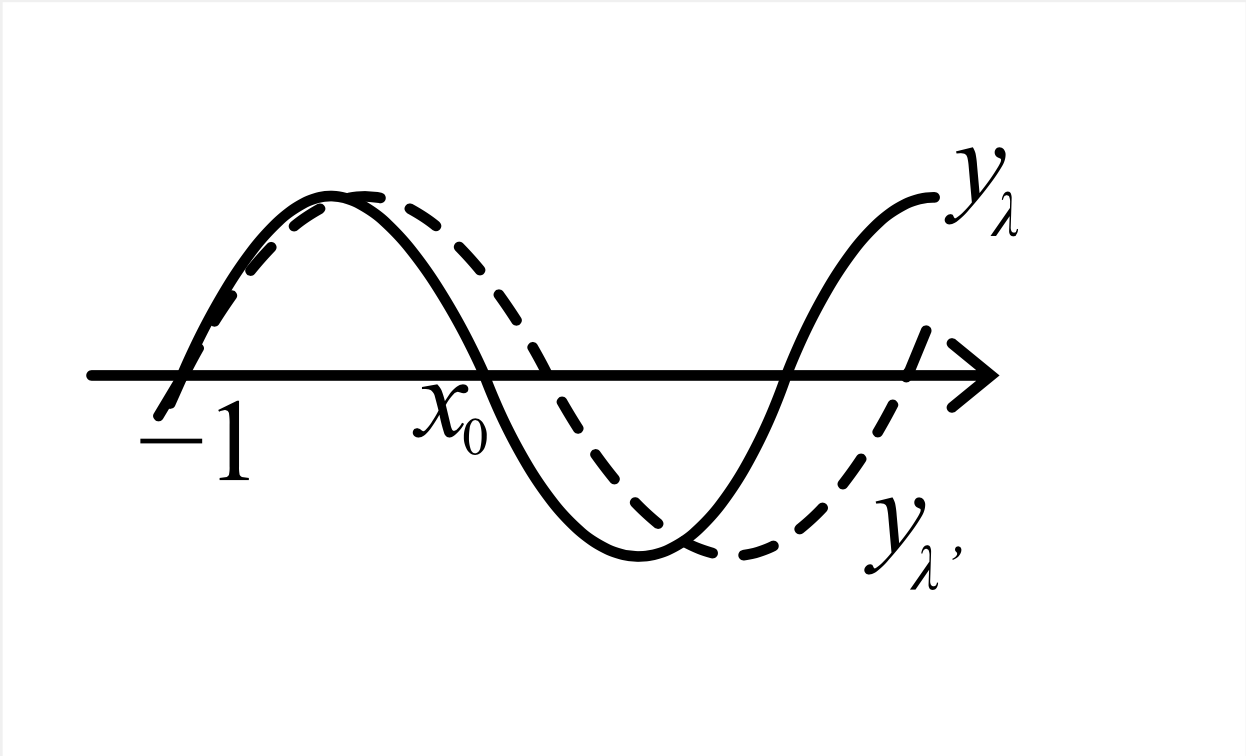
\(-1\leq x\leq x_0\) に \(y_{\lambda'}^m\) の零点がないと仮定すると、図2に示す通りこの範囲では \(y_\lambda^m, y_{\lambda'}^m\) ともに正です。 従って \[ DW = (\lambda'-\lambda)y_\lambda^my_{\lambda'}^m \gt0. \] ロンスキアンの初期値が \(W(x=-1)=0\) ですから、\(W>0\;(-1\leq x\leq x_0)\) が得られます。 一方図2からもわかるとおり、\(y_\lambda^m\) は \(x_0\) 近傍で減少関数です。 \eqref{Wronskian}より、\(y_\lambda^m\) の零点 \(x_0\) にて \begin{array}{rclc} W(x_0) &=& (1-x_0^2)(y_{\lambda'}^mDy_\lambda^m-0) & \because y_\lambda^m(x_0)=0 \\ &\lt&0 \end{array} となり矛盾します。 よって \(y_{\lambda'}^m\) の零点の数は \(y_\lambda^m\) より多いことがわかりました。

以上より、\(l\) は \(|m|\) を下回らない整数であることが必要だとわかりました。 本節で得られた条件をまとめると、 \begin{align} \tag{6.11} &\lambda=l(l+1) \\ \tag{6.12} &l\in\mathbb{Z}_{\geq0} \\ \tag{6.13} &l\geq|m| \end{align} です。