11.1.1 ルジャンドル多項式の級数表示

結論から言えば、 \[ \tag{11.2} \label{Leg series} P_n(x) = \sum_{r=0}^{[n/2]} \dfrac{(-1)^r(2n-2r)!}{2^nr!(n-r)!(n-2r)!} x^{n-2r} \] です。 ただし \([n/2]\) はガウス記号と呼ばれ、\(n/2\) を超えない最大整数と定義されます。

導出は\eqref{def}を \(t,x\) でテイラー展開して \(t^n\) の係数を比較すればできます。 その際、\(y:=2tx-t^2\) とすると見通しがいいでしょう。 \begin{array}{rcl} g(t,x) &=& (1-y)^{-1/2} \\ &=& 1 + \dfrac{1}{2}y + \dfrac{1}{2}\dfrac{3}{2} \dfrac{y^2}{2!} + \dfrac{1}{2}\dfrac{3}{2}\dfrac{5}{2} \dfrac{y^3}{3!} + \cdots \\ &=& \displaystyle \sum_{p=0}^\infty \frac{(2p-1)!!}{2^p}\dfrac{y^p}{p!} \\ &=& \displaystyle \sum_{p=0}^\infty \frac{(2p)!}{2^{2p}(p!)^2}y^p . \end{array} また \(y^p=(2tx-t^2)^p\) を2項展開すると、 \begin{array}{rcl} y^p &=& t^p(2x-t)^p \\ &=& \displaystyle t^p\sum_{r=0}^\infty \left(\begin{matrix}p\\r\end{matrix}\right) (2x)^{p-r} (-t)^r \end{array} となるので、 \[ g(t,x) = \sum_{p=0}^\infty \sum_{r=0}^p \dfrac{(2p)!}{2^{2p}(p!)^2}t^p \dfrac{p!}{(p-r)!r!} (2x)^{p-r}(-t)^r . \] \(t^n\) の展開係数を見るために \(p+r=n\) となる \(p,r\) を取り出せば、 \[ g(t,x) = \sum_r \dfrac{(2n-2r)!(-1)^rx^{n-2r}}{2^n(n-r)!r!(n-2r)!} t^n \] となります。 ここで、\(0\leq r\leq p=n-r\) より \(0\leq r\leq[n/2]\) ですから、\eqref{Leg series}が得られます。

11.1.2 ロドリゲスの公式と母関数

数々の直交関数で威力を発揮するロドリゲスの公式というものがあります。 そのシステマティックな使い方は主に§7で解説しているのでそちらに回すとして、ここではルジャンドル多項式の表示を提示し、11.2の議論につなげていきます。

ロドリゲスの公式によって \(n\) 次のルジャンドル多項式は \[ \tag{11.3} \label{Leg Rodrigues} P_n(x) = \dfrac{1}{2^nn!} \dfrac{d^n}{dx^n}(x^2-1)^n \] と表せます。 この表式が\eqref{Leg series}に一致することを確かめましょう。 \((x^2-1)^n\) を2項展開すると、 \[ \tag{11.4} \label{11.4} \dfrac{1}{2^nn!}D^n(x^2-1)^n = \dfrac{1}{2^nn!}D^n\sum_{r=0}^n \left(\begin{matrix}n\\r\end{matrix}\right) (x^2)^{n-r}(-1)^r \] となります。 \[ D^nx^{2n-2r} = \dfrac{(2n-2r)!}{(n-2r)!}x^{n-2r} \] ですから、\eqref{11.4}の右辺が \(r\gt n/2\) で \(0\) となることに注意して、 \[ \dfrac{1}{2^nn!}D^n(x^2-1)^n = \sum_{r=0}^{[n/2]} \dfrac{(-1)^rn!(2n-2r)!}{2^nn!(n-r)!r!(n-2r)!} x^{n-2r} \] となり、\eqref{Leg series}に一致しますね。

ロドリゲスの公式によるルジャンドル多項式の表示\eqref{Leg Rodrigues}は定義式のテイラー展開係数\eqref{Leg series}と等価であることが示されましたから、\eqref{Leg series}の代わりに\eqref{Leg Rodrigues}を\eqref{def}の展開係数として以下の議論を進めていきます。

11.2.1 収束範囲の選択

さて、4.5で見たような状況では、 \begin{array}{rcl} \phi(\boldsymbol{x}) &=& \displaystyle\int_V d^3x' \dfrac{1}{4\pi\varepsilon} \dfrac{\rho(\boldsymbol{x}')}{\sqrt{x^2+x'^2-2xx'\cos\theta}} \\ &=& \displaystyle \dfrac{1}{4\pi\varepsilon x} \int_V d^3x' \dfrac{\rho(\boldsymbol{x}')}{\sqrt{1+\left(\dfrac{x'}{x}\right)^2-2\dfrac{x}{x'}\cos\theta}} \end{array} の右辺分母を \(x'/x\) の級数として \[ \phi(\boldsymbol{x}) = \dfrac{1}{x} \sum_n \int_V d^3x' \rho(\boldsymbol{x}')a_n(\cos\theta) \left(\dfrac{x'}{x}\right)^n \] の形に展開したいのでした。 \(x'\) は小領域 \(V\) 内部の点から原点までの距離であり、\(x\) は観測点から原点までの距離です。 多重極展開の文脈では「電荷分布を遠くの観測点から見たときに、電荷分布を点電荷や電気双極子などに近似できる」ということを示すので、\(x'\ll x\) とします。 とはいえ、どれほどのオーダー差をもって \(x'\ll x\) とするかは注目したい現象によりけりなので、ここでは \(x'\lt x\) としておくのが良いでしょう。

(4.6)を考慮すれば、\(-1\leq\cos\theta\leq1\) と合わせて考えると、\eqref{def}でいうところの \(|x|\leq1,|t|\lt1\) で級数が収束すれば実用上困ることはないでしょう。

11.2.2 複素積分を用いたルジャンドル多項式の導出

ロドリゲスの公式を使うと複素積分によってルジャンドル多項式の母関数が\eqref{def}の左辺になることが示せます。 その過程で11.2.1で議論した「\(|x|\leq1,|t|\lt1\) で級数が収束すること」を示していきます。 複素積分を使う方法では大まかな方針は同じですが、ここでは絶対収束などの細かい部分にまでこだわりを見せる時弘の方法を紹介しましょう。

ここで使うのがグルサの定理 \[ f^{(n)}(x) = \dfrac{n!}{2\pi i} \oint_C\dfrac{f(z)}{(z-x)^{n+1}}dz \] です。

この公式の条件は \(f\) が閉曲線 \(C\) で囲まれる領域 \(D\) 内部で正則であることでした。 \((z^2-1)^n\) は全平面で正則ですから、ロドリゲスの公式で表されたルジャンドル多項式\eqref{Leg Rodrigues}に適用すると、 \[ \tag{11.5} \label{Schlaefli} P_n(x) = \dfrac{1}{2^nn!}D^n(x^2-1)^n = \dfrac{1}{2\pi i} \oint_C\dfrac{(z^2-1)^n}{2^n(z-x)^{n+1}}dz \] となります。

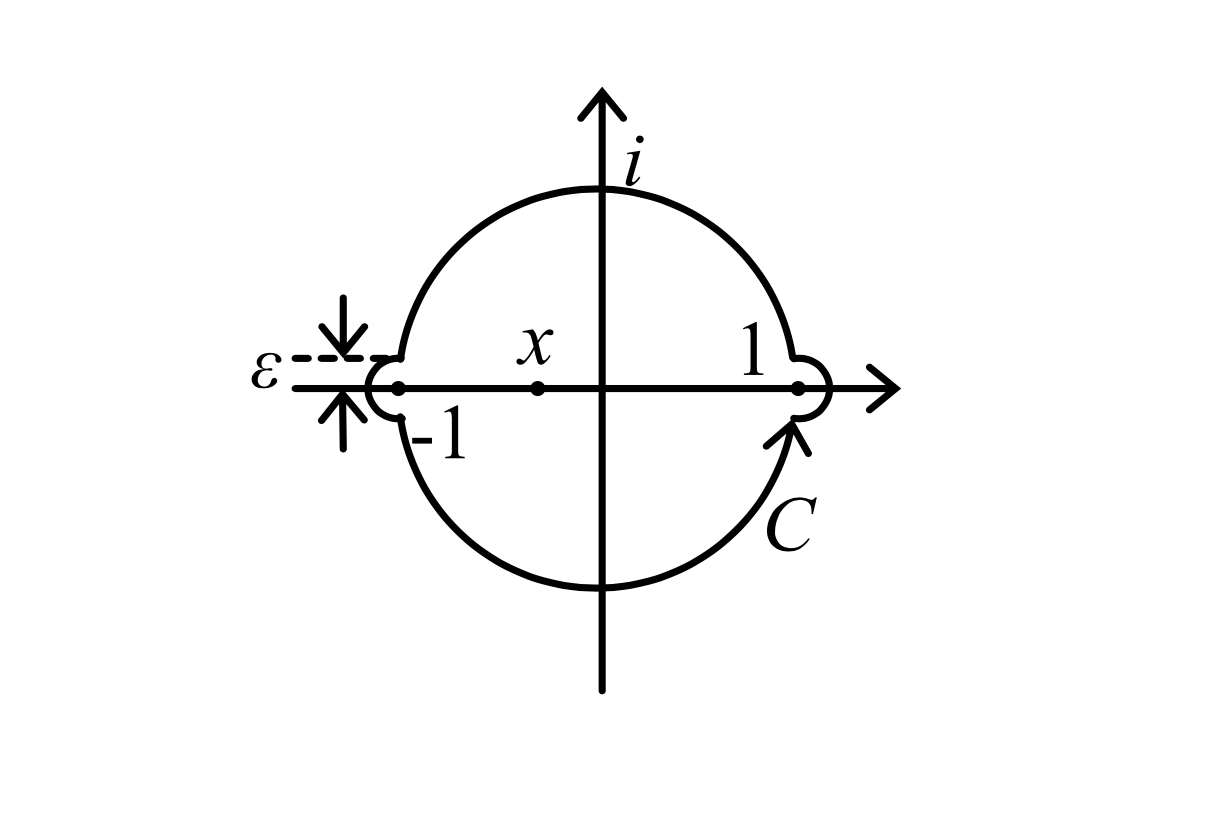
\(-1\leq x\leq1\) を扱いたいので、図3に示すような単位円及び \(\pm1\) の周りで微小半径 \(\varepsilon\ll1\) の円弧形迂回路を \(C\) として取ります。

母関数展開\eqref{def}の形に持ち込むために、\eqref{Schlaefli}の無限級数を取ります。 \[ \tag{11.6} \label{11.6} \sum_{n=0}^\infty P_n(x)t^n = \sum_{n=0}^\infty \dfrac{1}{2\pi i} \oint_C\dfrac{(z^2-1)^n}{2^n(z-x)^{n+1}}t^ndz \]

ここである程度の方針を立てておきましょう。 母関数 \[ \tag{11.7} \label{g} g(t,x) = \dfrac{1}{\sqrt{1-2tx+t^2}} \] は無限級数の形をしていませんから、何かしらの形で級数を計算しなければなりません。 無限級数の結果がダイレクトに\eqref{g}の形になることは考えにくいですね。 おそらく計算過程で積分と無限級数の順序が入れ替わっていて、級数を計算して得られる関数を積分すると\eqref{g}が得られるのでしょう。 無限級数と積分の順序交換は、被積分関数が領域内で一様収束するときに限り可能なのでした。 被積分関数を眺めてみると \[ \tag{11.8} \label{11.8} \dfrac{t^n(z^2-1)^n}{2^n(z-x)^{n+1}} = \dfrac{1}{z-x} \left( \dfrac{t(z^2-1)}{2(z-x)} \right)^n \] となっていますから、 \[ \tag{11.9} \label{11.9} \left| \dfrac{t(z^2-1)}{2(z-x)} \right| \lt1 \] となれば間違いなく一様収束します。 さらにこの場合、積分と級数の順序交換をした後の無限級数が \(1\) より小さい数の \(n\) 乗の和になっているので、級数は容易に計算可能です。 ということで、以下では\eqref{11.9}を示していきます。

まずは分子を上から押さえます。 \(z\) が単位円上にあるとき、図4に示すように、\(z,\pm1\) の3点を頂点とする三角形は \(z\) の角で直角となりますね。 \(|z^2-1|=|z-1||z+1|\) というのは、この直角三角形の面積の2倍になっています。 一方で直角三角形の面積は実軸を底辺としたときに \(|\Im z|\) と表せますね。 \eqref{11.9}分母の \(z-x\) と打ち消しあってくれると助かるので、 \[ |z^2-1|=2|\Im z|\leq2|z-x| \] と押さえます。 \(|t|\lt1\) と合わせると、\(z\) が単位円上にある間は \[ \left| \dfrac{t(z^2-1)}{2(z-x)} \right| \leq|t| \lt1 \] です。

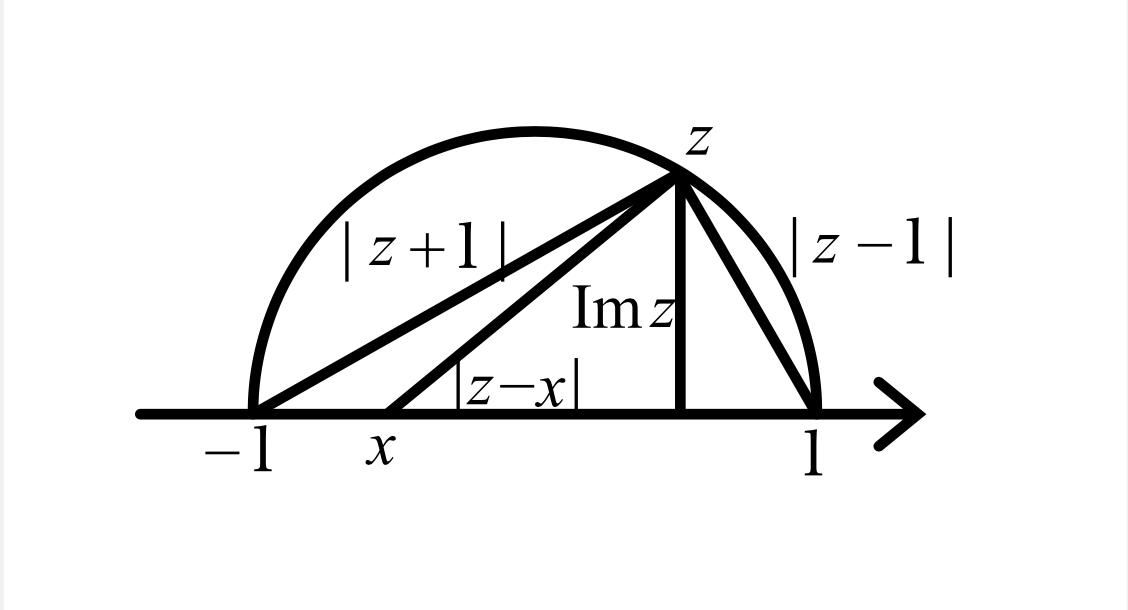
問題は \(z\) が \(\pm1\) 周りの微小円上にあるときです。 先に \(1\) 周りの円弧上を考えましょう。 一般に \(-1\leq x\leq1\) で \(|z-1|\leq|z-x|\) ですから、 \[ \left| \dfrac{t(z^2-1)}{2(z-x)} \right| \leq \dfrac{|t(z^2-1)|}{|2(z-1)|} = \left| \dfrac{t(z+1)}{2} \right| \] が成り立ちます。 \(z=1+\varepsilon e^{i\theta}\) のように表されるので、\(|z+1|\leq|2+\varepsilon|\) です。 ゆえに \[ \left| \dfrac{t(z^2-1)}{2(z-x)} \right| \leq \left| \dfrac{t(z+1)}{2} \right| \leq \left| \dfrac{t(2+\varepsilon)}{2} \right| . \] \(|t|\lt1\) としていますから、右辺の値が \(1\) を下回るような \(\varepsilon\gt0\) は存在します。 \(-1\) 周りも全く同様です。

以上によって、\(\forall z\in C\) で\eqref{11.9}が成り立つことがわかりました。 先ほど考察した通り\eqref{11.8}が \(|t|\lt1, |x|\leq1\) で一様収束しますから、\eqref{11.6}の級数と積分順序が交換できて、 \[ \sum_{n=0}^\infty P_n(x)t^n = \dfrac{1}{2\pi i} \oint_C \sum_{n=0}^\infty \dfrac{(z^2-1)^n}{2^n(z-x)^{n+1}}t^ndz \] です。 \eqref{11.8}の級数を計算すれば、 \begin{array}{rl} & \displaystyle \dfrac{1}{z-x} \sum_{n=0}^\infty \left( \dfrac{z^2-1}{2(z-x)}t \right)^n \\ =& \dfrac{1}{z-x} \dfrac{1}{1-\dfrac{z^2-1}{2(z-x)}t} \\ =& \dfrac{1}{-\dfrac{t}{2}z^2+z-x+\dfrac{t}{2}} \\ =& -\dfrac{2}{t}\dfrac{1}{(z-z_+(x))(z-z_-(x))} \end{array} となります。 ただし \(z_\pm(x)\) は \[ z^2-\dfrac{2}{t}z-1+\dfrac{2}{t}x=0 \] の解で、具体的に計算すると \[ z_\pm(x) = \dfrac{1\pm\sqrt{1+z^2-2tx}}{t} \] です。 特に、\(C\) 内部にあるのは \(z_-(x)\) に限られます。 よって留数定理から、 \begin{array}{rl} & \displaystyle \frac{1}{2\pi i} \oint_C -\frac{2}{t}\frac{1}{(z-z_+(x))(z-z_-(x))}dz \\ =& -\dfrac{2}{t}\dfrac{1}{2\pi i} \cdot 2\pi i\dfrac{1}{z_-(x)-z_+(x)} \\ =& -\dfrac{2}{t}\dfrac{t}{-2\sqrt{1+t^2-2tx}} \\ =& \dfrac{1}{\sqrt{1+t^2-2tx}} \end{array} となって、母関数\eqref{g}が導出されました。